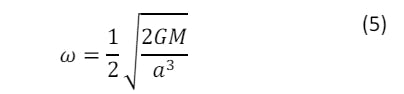Isaac Asimov’s Celestial Puzzle: How Six Suns Shape Kalgash
Table of Links
Abstract and 1 Introduction
2. Summary of the Story
3. Observables
4. Possible Scenarios and Consequences
The other Suns
Simulation
Conclusion and References
4. POSSIBLE SCENARIOS AND CONSEQUENCES
The most important constraint is that of the red star Dovim. This is the only star visible in that crucial time just before the deadly eclipse and the plot hinges on two factors:
1. Dovim is bright enough to blot out the other stars in the Universe.
2. The eclipse lasts for a period of 9 hours at the equator, sufficient that the entire planet is covered in darkness.
If we look at the case of our own Earth, the Sun has an apparent magnitude of -26.74 (Williams, 2004) and the faintest object visible to the naked eye during the day is -4.00 magnitudes (Wikipedia, 2014, http://en.wikipedia.org/wiki/Apparent_magnitude) for a difference of about 22.5 magnitudes. We will assume that Dovim is bright enough to blot out 0th magnitude stars and hence must be brighter than magnitude -22.5. This puts the star at a distance of about 44 light minutes from the Onos (Kalgash’s primary star). The distance of the star from Kalgash would then vary from 34 to 54 light minutes and the star’s angular diameter as observed from the planet would vary from 3 to 5 arcminutes.
The eclipse of Dovim by Kalgash 2 as seen from the planet lasts a minimum of 9 hours, compared to a solar eclipse on the Earth of less than 8 minutes (Meeus, 2003). Our Moon is about the same size as our Sun but Asimov does mention that the angular diameter of Kalgash 2 is seven times that of Dovim or about 2°. The orbital period of the Moon can be calculated from Kepler’s Laws.
We can derive the equation of motion of Kalgash and Kalgash 2 by equating the gravitational force to the centripetal force (we consider M1):
Since M1 and M2 orbit around their centre of mass, we can write:
We insert this result into (1):
We have considered a circular orbit, but the result is also valid for an ellipse. In that case, d is replaced with a, the semi-major axis. If M1 = M2 = M, then we get:
Now, we can calculate the angular speed of Kalgash 2, with respect to Kalgash:
During the eclipse, Kalgash 2 will cover a total angular distance of:
We summarise the results in the following graph (Figure 3) for a Kalgash 2 of Earth-mass.
We have a constraint on the size of Kalgash 2 from the stated fact that its angular diameter at the time of eclipse is 7 times that of Dovim. We have already assumed that the mass of the planet and the moon are the same as that of the Earth which thereby sets the diameter of the moon as a function of its density. If this density were the same as that of our own Moon, Kalgash 2 would be relatively small and close to the planet and therefore would move rapidly along its orbit resulting in short eclipses. On the other hand, if the density of Kalgash 2 were closer to that of the gas giants, the radius of the moon would be much larger and thus its distance from Kalgash would be much greater while
maintaining the same angular diameter. Then by Kepler’s Third Law, it would move more slowly along its orbit and the eclipse duration would be correspondingly longer. We find that a moon with a density the same as Saturn (~0.7 gm/cm3) (Williams, 2006) would eclipse Dovim for 9 hours, more than enough time to cover the entire planet with darkness. By comparison, the majority of the satellites in our Solar System have densities of 1.5 – 3 gm/cm3 (Williams, 2014)with the least dense large moon being Tethys with a density of 0.9 gm/cm3 (Roatsch, et al., 2009).
THE OTHER SUNS
ONOS
Onos is the parent sun of Kalgash. It gives off a bright yellow light, therefore it must be a Sun-like star. However, it is slightly further away than our own sun, at a distance of 1.2AU. Onos would appear dimmer by a factor of 1.44, or like a bright day in Sao Paulo.
TANO-SITHA
Tano-Sitha are also a white binary pair, further yet brighter than Trey – Patru. This indicates that they could be massive A-type stars or white dwarves.
A-type Stars
Since we want to minimise tidal effects, we shall suppose that they are A9V types at a temperature of 7100K, radius of 1.55 solar radii and 1.62 solar masses. This binary is at the edge of the Kalgash universe at a distance of 110 light minutes. It will have an apparent magnitude of -23.7, much brighter than Dovim! But Asimov mentions that they produce light much fainter than Dovim. They cannot be A-type Stars.
White Dwarfs
In this case, we suppose the stars are similar to Sirius B. They have a surface temperature of 25200K, a radius similar to that of Earth (6370km) and are at a distance of 110 light minutes. Then the apparent magnitude is -18.09 or about 114 times brighter than the full moon.
TREY-PATRU
The secondary binary also produces white light. However, it is closer to Onos than Tano-Sitha, but fainter. The only way this is possible is if it is a cool white dwarf, similar to 40 Eridani B. Then the stars will have a temperature of 16500K, a radius of 0.014 Solar radius and a mass of 0.50 solar mass. At a distance of 100 light-minutes, the apparent magnitude of the binary is -17.38, or around 59 times brighter than the moon.